Recurrent Neural Network (RNN)

RNN intuition

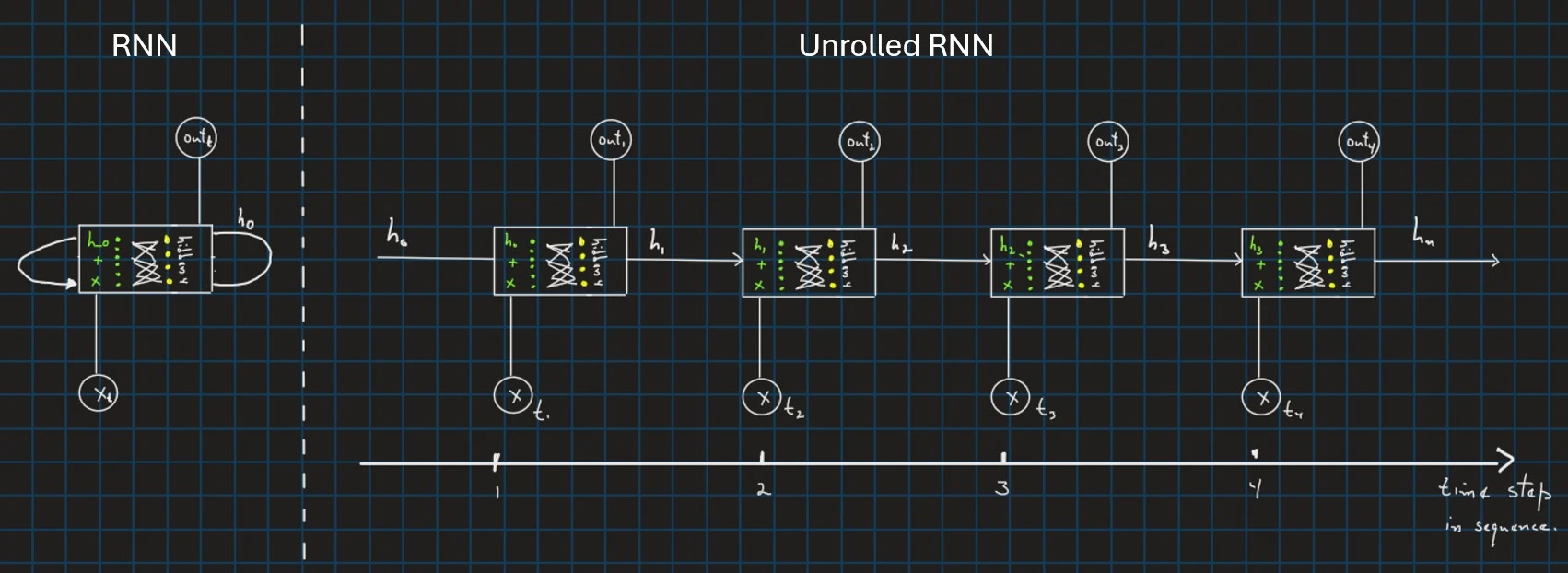
When I first began exploring RNN architecture, I struggled with understanding how they utilize the same neural layer across time steps to process sequential data. Essentially, it’s like moving through the sequence of time steps using the same layer. This ‘hidden state’ from the previous time step, represented as $h$, is crucial. At each time step $t$, the RNN takes in two inputs: the current value in the sequence, $x_t$, and the previous hidden state, $h_{t-1}$. It then produces two outputs: the current hidden state, $h_t$, and the output, $o_t$. This flexibility allows practitioners to decide how to use the outputs at each step in the sequence. For example, one might choose to feed all outputs into a dense layer or select only the outputs from the last few time steps. This ability of RNNs to process both the current value $x_t$ and the previous computed value $h_{t-1}$ makes them well-suited for handling sequential data.

Inside of the RNN Cell

In the figure above, each square will be called “RNN cell”. At this stage, my question was, if RNN is a neural network that takes as input the current sequence value plus some calculated value from priors time steps $h{t-1}$, How many layers do this neural network has? what exactly happen inside of the RNN cell?

I mostly use PyTorch, which includes the Jeff Elman RNN.

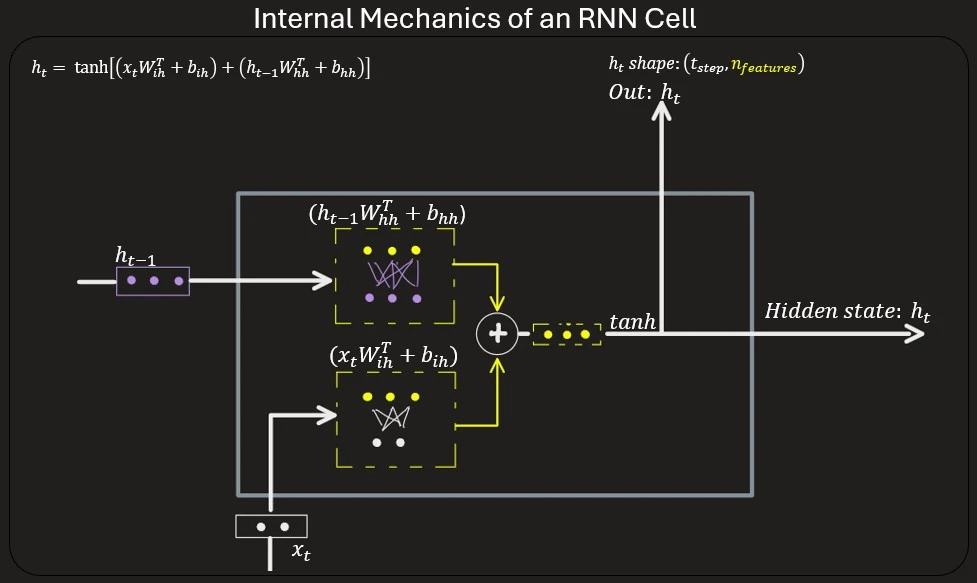
\[h_t = tanh(x_tW_{ih}^T + b_{ih} + h_{t-1}W_{hh} + b_{hh})\]

In this notation, we have two weight matrices, $W_{ih}$ that multiply the sequence input $x_t$ and the $W_{hh}$ that multiply the prior hidden state $h_{t-1}$. This means that each input ($x_t$ and $h_{t-1}$) is initially processed independently by a layer of neurons and their biases. The outputs of these two neural networks (of one layer) are then combined through an element-wise addition operation (matrix addition). This aggregated result is passed through an activation function (e.g., tanh) to produce the final output $h_t$, which follows two paths as shown in the figure above. The shape of $h_t$ will be $(\text{time_step}, \text{number_of_features})$, where the number of features corresponds to the number of neurons in this shared layer for both networks. So, based on this info, inside of the RNN there are two neural network, both has one layer with the same number of neurons.

The figure above illustrates a sequence where $x$ has two features, and we decide that the number of neurons in each hidden layer is three. If our input sequence has four time steps, the final output shape after running the RNN will be $(4, 3)$.

For a deeper diving in Neural Network mathematical notation, check this post Neural Network Mathematical Notation

Quick Pytorch Visualization

With the following Python code using PyTorch you can start experiment/playing with this.

Code Here

#________________________________________
# IMPORT LIBRARIES
import torch
import torch.nn as nn


#________________________________________
# GENERATING RANDOM SEQUENCE 
n_features  = 2 # number of features in x 
time_step = 4   # time step
batch_size = 1  # number of sample
x = torch.randn(size=(batch_size, time_step, n_features))

print(f"x shape: {x.shape}\n") # >> torch.Size([1, 4, 2])


#________________________________________
# CREATE A RNN LAYER/ARCHITECTURE
n_neurons = 3
rnn_cell = 1
rnn = nn.RNN(input_size=n_features,     # number of columns/features for each time step
             hidden_size=n_neurons,     # num of neurons in NN layer inside the RNN cell
             bias=True,                 # neural layer will use bias? 
             num_layers=rnn_cell,       # num of stacked RNNs cells
             batch_first=True,          # shape of sequence input: (batch, time_step, n_features)
             bidirectional=False,       # transfrom RNN in bidirectional
            )


#________________________________________
# FOWARD PASSING OF SEQUENCE "x"

# rnn return 
# >>> out is shape (batch=1, time_step=4, out_weights=3)
# >>> h_n is last hidden weights for each RNN layer in the last step
print("running rnn ...\n")
out, h_n = rnn(x)
print(f"out_shape: {out.shape}, \nlast h_n shape: {h_n.shape}")